Dubbelverhouding
In de meetkunde is de dubbelverhouding van vier collineaire punten gedefinieerd als de verhouding van twee deelverhoudingen. De dubbelverhouding is invariant onder centrale projectie.
Definitie
De dubbelverhouding van de vier collineaire punten en in de euclidische ruimte, genoteerd als of is gedefinieerd als het quotiënt van de deelverhoudingen en :
Als en de coördinaten zijn van respectievelijk en op de rechte als getallenrechte, wordt de dubbelverhouding:
De dubbelverhouding is positief als de deelpunten en ofwel allebei op het lijnstuk ofwel allebei buiten het lijnstuk liggen. Ligt een van de punten op het lijnstuk en een erbuiten, dan is de dubbelverhouding negatief.
Verwisselt men en of en , dan verandert de dubbelverhouding in zijn omgekeerde, dus
Verwisselt men en , dan krijgt men
Vier punten op een lijn hebben dus zes verschillende waarden als dubbelverhouding, namelijk:
- en
Bij vier punten op gelijkmatige afstand en in volgorde krijgen we bijvoorbeeld 4. De andere vijf waarden zijn dan 1/4, -3, -1/3, 3/4 en 4/3.
Harmonische ligging
Als de punten en het lijnstuk respectievelijk inwendig en uitwendig in dezelfde verhouding verdelen, geldt voor de deelverhoudingen
- ,
dus voor de dubbelverhouding
Men zegt dat de vier punten in harmonische ligging zijn.
De volgende uitspraken zijn gelijkwaardig:
- Het geordende viertal punten is een harmonisch puntenviertal.
- De dubbelverhouding .
- De punten en liggen harmonisch ten opzichte van de punten en .
- Het punt is harmonisch toegevoegd aan of harmonisch verwant met het punt ten opzichte van de punten en .
Voorbeelden
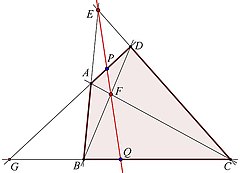
(EFPQ) = -1
- Van de hoeken tussen twee snijdende rechten en zijn en de bissectrices. De rechte snijdt de vier rechten en in opvolgend de punten en . De punten en zijn dan harmonisch toegevoegd ten opzichte van de punten en .
- Een lijn door twee diagonaalpunten van een volledige vierhoek snijdt de overige zijden in twee punten die ten opzichte van die diagonaalpunten harmonisch liggen (zie de figuur hiernaast).
- De binnen- en buitenbissectrice van een hoek van een driehoek snijden de overstaande zijde van die hoek in punten die harmonisch toegevoegd zijn ten opzichte van de hoekpunten op die zijde.
Eigenschappen

De dubbelverhouding is invariant onder centrale projectie, dus als en twee stellen collineaire punten zijn, en de lijnen en concurrent zijn, geldt .
Dubbelverhouding van lijnen
Door de invariantie van de dubbelverhouding onder centrale projectie kan de dubbelverhouding ook gedefinieerd worden voor concurrente coplanaire rechten. Snijden de door hetzelfde punt gaande rechten en een rechte in vier niet-samenvallende punten en , dan is de dubbelverhouding gedefinieerd als
Alternatieve definitie
Een alternatieve equivalente definitie voor de dubbelverhouding van vier concurrente rechten is
Harmonische vierstraal
Een vierstraal is een geordend viertal coplanaire, concurrente rechten. Een vierstraal heet harmonisch dan en slechts dan, als . De volgende uitspraken zijn dan gelijkwaardig:
- De vierstraal is harmonisch.
- De dubbelverhouding .
- De lijnen en liggen harmonisch ten opzichte van de lijnen en .
- Lijn is harmonisch toegevoegd aan lijn ten opzichte van de lijnen en .
Voorbeelden
- Twee snijdende rechten en liggen harmonisch ten opzichte van de bissectrices en van de hoeken die ze met elkaar maken.
- Twee diagonalen van een volledige vierhoek zijn harmonisch toegevoegd ten opzichte van de zijden door hun snijpunt
- De poollijn van een punt , ten opzichte van de rechten en met snijpunt , is de lijn die harmonisch is toegevoegd aan de lijn ten opzichte van de lijnen en .
Dubbelverhouding op een kegelsnede

Verbindt men een veranderlijk punt van een niet ontaarde kegelsnede met vier vaste punten van , dan verkrijgt men een veranderlijke vierstraal met constante dubbelverhouding. Die dubbelverhouding is enkel afhankelijk van de stand van de vier punten op de kegelsnede en wordt de dubbelverhouding van die vier punten genoemd.
Snijdt men vier vaste raaklijnen aan een niet ontaarde kegelsnede met een veranderlijke raaklijn aan , dan verkrijgt men een puntenviertal met constante dubbelverhouding. Die dubbelverhouding is enkel afhankelijk van de stand van de vier vaste raaklijnen en wordt de dubbelverhouding van die vier raaklijnen genoemd.
Op de figuur zijn de rechten en vaste raaklijnen en de punten en vaste punten op de kegelsnede.
De dubbelverhouding is onafhankelijk van de stand van het punt op de kegelsnede, daardoor is de dubbelverhouding ondubbelzinnig bepaald. Zo is ook onafhankelijk van de stand van de veranderlijke raaklijn en is de dubbelverhouding van de vier vaste raaklijnen correct gedefinieerd.
Zie ook
- Harmonische ligging
- Projectieve lijn
- Lijnperspectief

























































 Dubbelverhouding
Dubbelverhouding